Article Sidebar

Download
PDF
Statistic
Read Counter : 125 Download : 148

Main Article Content

Abstract

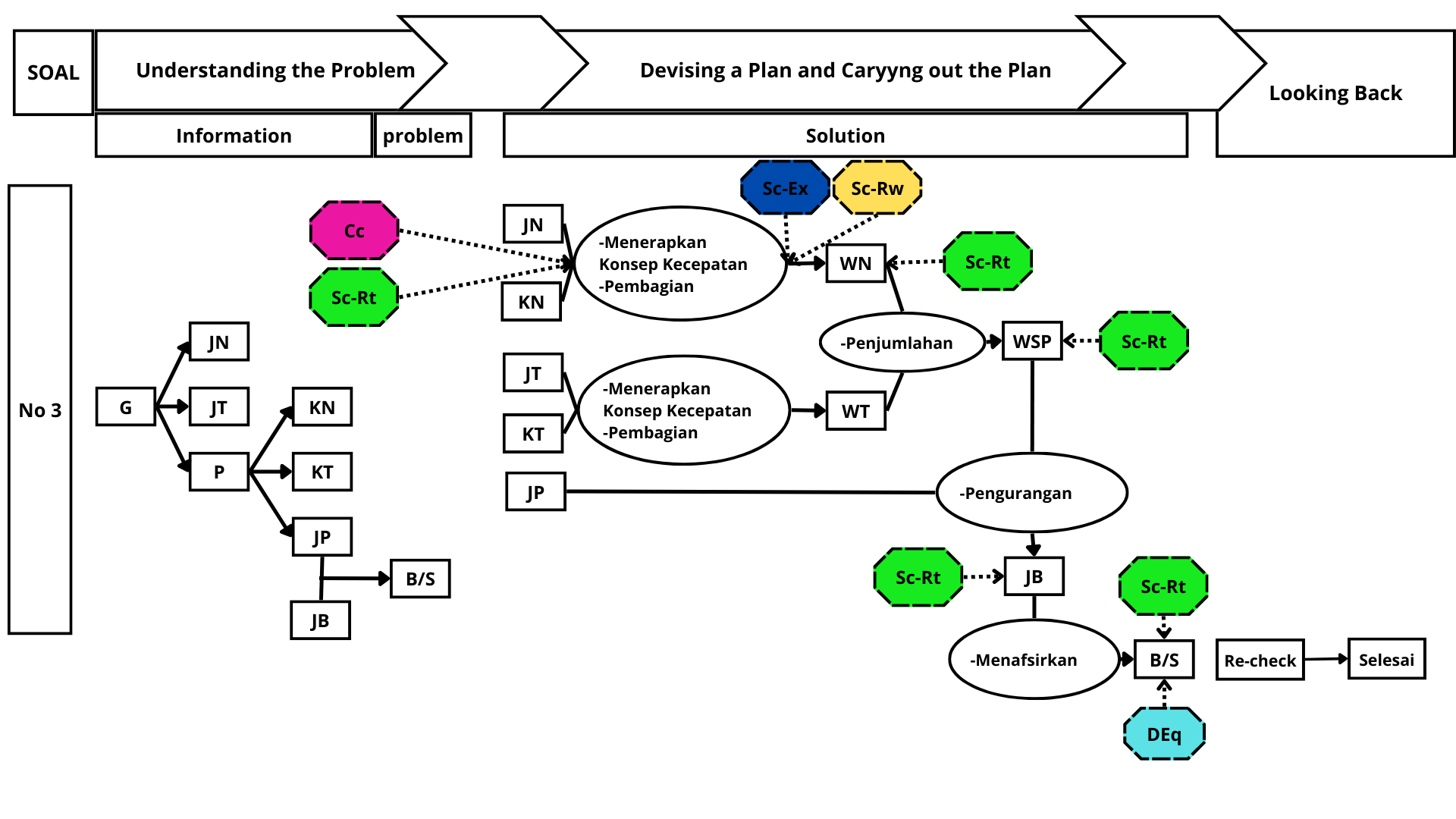
Errors in problem solving indicate that there are parts of the cognitive structure that are problematic, either because they are disorganized, disconnected or experiencing cognitive holes. thinking This research uses a qualitative approach. The data analysis technique used refers to the Miles and Huberman analysis model, namely data reduction, data presentation and finally drawing conclusions. The results showed that the three subjects studied were only S1 subjects who were able to answer all the questions given correctly without going through the defragmenting process, this was because the problem-solving thinking structure of the questions was classified as good, this success was supported by the level of cognitive understanding of the prerequisite material for the questions. good. While on the subject of S2, even though the conclusions of the answers already look correct, in one of the questions, it appears that there is an error in thinking which is categorized as pseudo, this error occurs because of the tendency to only pursue similarity questions and do not emphasize understanding mathematical concepts. The defragmenting efforts given are in the form of cognitive conflict interventions, scaffolding–restructuring and scaffolding explaning. While on the subject of S3, the low literacy ability in reading the test questions, as well as understanding the concept of the prerequisite material for the questions, causes errors at all stages of problem solving. The defragmenting efforts given are scaffolding-explaning intervention, scaffolding restructuring, cognitive conflict, scaffolding-review, disequilibration. The lack of knowledge about the prerequisite material so that more emphasis is placed on providing scaffolding-explaning.

Keywords

DefragmentingThinking StructureProblem SolvingPISA

Article Details

How to Cite
Wahab A, A., Buhaerah, Ahsan, M., & Busrah, Z. (2022). DEFRAGMENTING THE THINKING STRUCTURE OF PROBLEM SOLVING THROUGH COGNITIVE MAPPING BASED ON POLYA THEORY ON PISA PROBLEMS. Journal of Mathematics Learning Innovation, 1(1), 93–97. https://doi.org/10.35905/jmlipare.v1i1.3388
Download Citation
Endnote/Zotero/Mendeley (RIS)
BibTeX

References

  1. Abadi, A. P., Subanji, S., & Chandra, T. D. (2017). Diagnosis kesulitan siswa dalam menyelesaikan masalah geometri-PISA melalui pemetaan kognitif dan upaya mengatasinya dengan scaffolding. MENDIDIK: Jurnal Kajian Pendidikan Dan Pengajaran, 3(1), 1–18.
  2. Allen, C. E., Froustet, M. E., LeBlanc, J. F., Payne, J. N., Priest, A., Reed, J. F., … Payne, J. N. (2020). National Council of Teachers of Mathematics. The Arithmetic Teacher, 29(5), 59. https://doi.org/10.5951/at.29.5.0059
  3. Anggraini, D., Kusmayadi, T. A., & Pramudya, I. (2018). The characteristics of failure among students who experienced pseudo thinking. Journal of Physics: Conference Series, 1008(1). https://doi.org/10.1088/1742-6596/1008/1/012061
  4. Anghileri, J. (2006). Scaffolding practices that enhance mathematics learning. Journal of Mathematics Teacher Education, 9(1), 33–52. https://doi.org/10.1007/S10857-006-9005-9
  5. Ani, E. U., & Rahayu, P. (2018). Profil Kemampuan Pemecahan Masalah Matematika Siswa Berbentuk Soal Cerita Materi Bangun Ruang. Jurnal Riset Pendidikan Dan Inovasi Pembelajaran Matematika (JRPIPM), 1(1), 40. https://doi.org/10.26740/jrpipm.v1n1.p40-49
  6. Brender, J. (2006). Framework for Meta-Assessment of As- sessment Studies Ethnographic research.
  7. Buhaerah, B. (2022). Scaffolding Through Cognitive Mapping Based on Diagnosing Student’S Difficulties in Solving Problem. Journal for the Education of Gifted Young Scientists, 10(8), 207–220. https://doi.org/10.17478/jegys.1099807
  8. Damayanti, P. A., Subanji, S., & Sukoriyanto, S. (2020). Defragmentasi Struktur Berpikir Siswa Impulsif dalam Memecahkan Masalah Geometri. Jurnal Pendidikan: Teori, Penelitian, Dan Pengembangan, 5(3), 290. https://doi.org/10.17977/jptpp.v5i3.13239
  9. Kholid, M. N., & Ahadiyati, A. (2022). Students’ metacognition in solving non-routine problems. Al-Jabar : Jurnal Pendidikan Matematika, 13(1), 125–138. https://doi.org/10.24042/ajpm.v13i1.11776
  10. Kumalasari, F., Nusantara, T., & Sa’dijah, C. (2016). Defragmenting struktur berpikir siswa dalam menyelesaikan masalah pertidaksamaan eksponen. Jurnal Pendidikan: Teori, Penelitian, Dan Pengembangan, 1(2), 246–255.
  11. Kurniati, D., Harimukti, R., & Jamil, N. A. (2016). Kemampuan berpikir tingkat tinggi siswa SMP di Kabupaten Jember dalam menyelesaikan soal berstandar PISA. Jurnal Penelitian Dan Evaluasi Pendidikan, 20(2), 142–155. https://doi.org/10.21831/pep.v20i2.8058
  12. Labuschagne, A. (2015). Qualitative Research - Airy Fairy or Fundamental? The Qualitative Report, 8(1), 100–103. https://doi.org/10.46743/2160-3715/2003.1901
  13. Lutfianto, M., Zulkardi, & Hartono, Y. (2013). Unfinished student answer in Pisa mathematics contextual problem. Journal on Mathematics Education, 4(2), 188–193. https://doi.org/10.22342/jme.4.2.552.188-193
  14. Matthew B. Miles, A. M. H. (1984). Qualitative Data Analysis. In International Legal Materials (Vol. 33). Newbury Park: SAGE Publication. https://doi.org/10.1017/s0020782900036494
  15. OECD. (2019). Programme for international student assessment (PISA) results from PISA 2018. OECD, pp. 1–10. Retrieved from https://www.oecd.org/pisa/publications/PISA2018_CN_IDN.pdf
  16. Partnership for 21st Century learning. (2015). 21st Century Student Outcomes. 1–9. Retrieved from http://www.p21.org/our-work/p21-framework
  17. Pranitasari, D., & Ratu, N. (2020). Analisis Kesalahan Siswa Dalam Menyelesaikan Soal Matematika Pisa Pada Konten Change and Relationship. AKSIOMA: Jurnal Program Studi Pendidikan Matematika, 9(4), 1235. https://doi.org/10.24127/ajpm.v9i4.2685
  18. Putra, Y. Y., Zulkardi, Z., & Hartono, Y. (2016). Pengembangan Soal Matematika Model PISA Konten Bilangan untuk Mengetahui Kemampuan Literasi Matematika Siswa. Jurnal Elemen, 2(1), 14. https://doi.org/10.29408/jel.v2i1.175
  19. Ratu Firdausi Rahman, I. R. D. N. (2021). Analisis Kesalahan Siswa Dalam Menyelesaikan Soal Pemecahan Masalah Matematika Berdasarkan Teori Newman. Hipotenusa Journal of Research Mathematics Education (HJRME), 4(2), 102–113. https://doi.org/10.36269/hjrme.v4i2.499
  20. Rofi’ah, N., Ansori, H., & Mawaddah, S. (2019). Analisis Kesalahan Siswa Dalam Menyelesaikan Soal Cerita Matematika Berdasarkan Langkah Penyelesaian Polya. EDU-MAT: Jurnal Pendidikan Matematika, 7(2), 120. https://doi.org/10.20527/edumat.v7i2.7379
  21. Subanji. (2015a). Teori Kesalahan Konstruksi Konsep dan Pemecahan Masalah Matematika (1st ed.). Malang: UM Press.
  22. Subanji. (2015b). Teori Kesalahan Kontruksi Konsep dan Pemecahan Masalah Matematika. Malang: UM Press.
  23. Subanji. (2016). Teori Defragmentasi Strukttur Berpikir (1st ed.). Malang: UM Press.
  24. Teresa, H., Zubaidah, Z., & Nursangaji, A. (2020). Kemampuan Menyelesaikan Soal Pisa Pada Konten Change and Relationship. Jurnal AlphaEuclidEdu, 1(2), 60. https://doi.org/10.26418/ja.v1i2.42879
  25. Utami, R. W., & Wutsqa, D. U. (2017). Analisis kemampuan pemecahan masalah matematika dan self-efficacy siswa SMP negeri di Kabupaten Ciamis. Jurnal Riset Pendidikan Matematika, 4(2), 166. https://doi.org/10.21831/jrpm.v4i2.14897
  26. Vinner, S. (1997). The Pseudo-Conceptual And The Pseudo-Analytical Thought Processes In Mathematics Learning. Educational Studies in Mathematics, 97–129. https://doi.org/10.1023/A:1002998529016
  27. Wahab, A. (2022). Penerapan Model Kooperatif Tipe Jigsaw Terhadap Peningkatan Keaktifan Belajar Matematika. Jurnal Ilmiah Pendidikan Matematika Al-Qalasadi, 10(1), 81–88. https://doi.org/10.32505/qalasadi.v6i1.3718
  28. Wibawa, A. (2017). Pseudo Siswa Dalam Memecahkan Masalah Limit Fungsi. Nasional Exchange of Expriences Teacher Quality Improvement Program.

Most read articles by the same author(s)

Similar Articles

You may also start an advanced similarity search for this article.